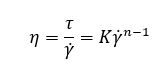CFD Project Vla: Viscosity
Bij Femto Engineering hebben we al heel wat Computational Fluid Dynamics (CFD) projecten gedaan. Maar we wilden verder kijken dan alleen de projecten die we voor onze klanten doen, dus hebben we besloten dat we verschillende situaties willen analyseren en simuleren en onze resultaten en analyses met jullie willen delen. Deze keer: Project Vla