Lineair statische sterkteberekeningen

Met dit artikel willen we je op een laagdrempelige wijze laten kennismaken met lineair statische sterkteberekeningen met behulp van de eindige elementen methode. Je kunt voor deze berekeningen FEA software (of 3D rekensoftware, EEM-, FEM- en simulatiesoftware) gebruiken zonder veel kennis te hebben van de opbouw en structuur van het programma. Handig als je snel aan de slag wilt, maar inzicht in de systematiek achter de software is vereist om resultaten juist te interpreteren en fouten snel te kunnen begrijpen en op te lossen. Daarom duiken we in het eerste deel van dit artikel in de eindige elementen methode. In het tweede gedeelte van dit artikel bespreken we de praktijk, toepassingen en de software.

De eindige elementen methode theorie

Laten we voorop stellen dat in de sterkteleer veel methoden en formules zijn ontwikkeld om de sterkte/stijfheid van een constructie te onderzoeken. Wij behandelen voor nu alleen de eindige elementen methode. Om het een en ander te visualiseren gebruiken we het voorbeeld van een brug. Als je deze brug ontwerpt, wil je weten welk effect krachten zoals verkeer en wind (belastingen) hebben op de constructie. Alle materialen veranderen van vorm als je er aan trekt of duwt. We zeggen dan ook dat elk materiaal in meer of mindere mate elastisch is. Bij een bepaalde kracht zal het materiaal daarom verlengen. Ook al zijn de vergelijkingen die de verdeling van structurele spanningen voor het gekozen materiaal beschrijven bekend, ze kunnen niet gelijk worden opgelost voor een constructie met een complexe of onregelmatige vorm, zoals een brug. De geldende differentiaal vergelijkingen kunnen echter wel opgelost worden voor simpele vormen zoals een rechthoek. Hier komen we dat ook gelijk uit bij de kern van de eindige elementen methode, waarbij je een gecompliceerde vorm vervangt door een ongeveer 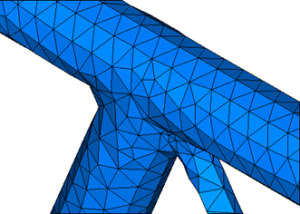gelijkwaardig netwerk van simpele elementen die met elkaar zijn verbonden middels knooppunten of nodes. Het patroon dat hierdoor ontstaat wordt de eindige elementen mesh genoemd. De eerste stap in de eindige elementen methode is om deze mesh te ontwerpen, hiervoor moet de beslissing gemaakt worden welke soort elementen gebruikt moeten worden.

Eindige element types bepalen

Een richtsnoer voor het bepalen van een elementtype: mesh een constructie zoveel mogelijk volgens zijn eigen opzet, bijv. een plaat met plaatelementen etc. Klik hier om te lezen waarop je de keuze voor 1D (lengte), 2D (gebied) of 3D (volume) elementen kunt baseren. In dit document vind je een handig overzicht van de elementtypes, kwaliteit van elementen en het aantal benodigde elementen. Interpolatiefuncties ofwel ‘shape functions’ bepalen hoe de spanningen binnen het element worden benaderd. Bij het gebruik van een eindige elementen programma worden de shape functions vastgelegd bij de keuze van het elementtype. Zoals je in onderstaande afbeelding kunt zien bepaald het aantal nodes in een element de orde van de shape functions (eerste orde of tweede orde).

De accuraatheid van de berekeningen hangt of van het aantal elementen en nodes dat gekozen wordt. Hoe meer elementen, hoe kleiner de elementen zijn en hoe accurater de resultaten, maar meer elementen en nodes betekent ook meer berekeningen. Daarom wordt altijd gezocht naar het optimale punt waar met net voldoende elementen, accurate resultaten worden bereikt binnen een redelijke tijd. Twee tips willen we hier nog meegeven. Het kan raadzaam zijn om een berekening op een lokaal punt te herhalen met een fijnere mesh om te controleren of de gewenste grootheden veranderen. Ook kunnen op lokale (kritieke) punten handberekeningen worden gedaan ter controle van het model.

Werking eindige elementen analyse

Laten we in het voorbeeld van de brug kiezen voor een eerste orde blok element (8 nodes). In het algemeen kan elke node zowel horizontaal als verticaal bewegen.De uitzonderingen zijn de elementen aan de buitenkant van de constructie. De brug zweeft niet in de lucht, maar is verankerd. Deze fixaties moeten worden meengenomen in de berekening om een juiste representatie te geven van het fysieke probleem. Tenslotte moeten de elastische eigenschappen van het materiaal worden gedefinieerd en de externe krachten die worden losgelaten op de constructie.

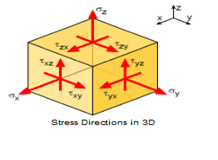
We beginnen vanuit de basisrelatie die de verplaatsing van een node uitdrukt als een functie van de X en Y coördinaten van de nodes. In ons voorbeeld met 8 nodes heb je voor elke node een vergelijking die de verplaatsing omschrijft als functie van de coördinaten. Dit geeft ons 8 vergelijkingen voor het gehele element. Deze vergelijkingen die de wiskundige relatie tussen opgelegde kracht en verplaatsing beschrijven kunnen we in een matrix plaatsen. We noemen dit de stijfheidsmatrix van het element. In plaats van een enkele verplaatsing op de X as, opereert een matrix op de vector X, waarvan de onderdelen de verplaatsingen van het gehele element uitdrukken. We voeren dit proces uit voor elk element in de mesh, zodat we voor elk element een stijfheidsmatrix krijgen. De volgende stap is om deze individuele matrices met elkaar te combineren in één grote matrix die de stijfheid van de hele constructie weergeeft. Elk element heeft knooppunten gemeen met een naburig element.

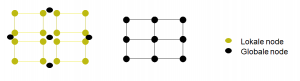Om dit principe simpel weer te geven illusteren we dit hier aan de hand van een 4-node plaatelement.

Gemeenschappelijke (of globale) knooppunten komen dus in beide matrices voor. De matrices kunnen daarom worden gecombineerd met een eenvoudige samenvoegingstechniek. In de praktijk wordt het oplossen van de gehele systeemvergelijking tegelijkertijd uitgevoerd met het combineren van de matrices. Er wordt vervolgens een standaard techniek gebruikt om delen van de matrix te elimineren. Dit proces noemen we reductie. We lossen de eerste vergelijking op en vullen de oplossing in bij de resterende vergelijkingen. Dit wordt herhaald tot we klaar zijn om de matrix van het volgende element toe te voegen. Wanneer het laatste element is toegevoegd hebben we de oplossing voor één enkele node in handen. 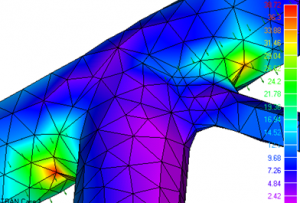We kunnen nu deze oplossing gebruiken als een sleutel en terugwerken door alle vergelijkingen van het systeem tot we alle verplaatsingen van elke node weten. Met deze resultaten kunnen we vervolgens snel de bijbehorende spanningen uitrekenen, die we vervolgens – met behulp van een postprocessor- met een contour diagram kunnen visualiseren.

Geen zorgen, FEA software neemt dit proces van verlengen en verplaatsingen met elkaar in verband brengen en de bijbehorende spanningen uitrekenen voor je uit handen. We kunnen met de software heel gemakkelijk de externe belasting verschuiven en zien wat dan de effecten zijn op de constructie. Omdat je zodoende allerlei scenario’s en testen kunt los laten op de constructie, omschrijven wij ons werk ook wel als virtueel prototypen of simulation. Je kunt je voorstellen dat uitvoerige simulatietesten, de kosten van fysieke testen aanzienlijk kan drukken.

FEA proces in kaart

Sterkteberekeningen software

Voordat er FEA software bestond werden sterkteberekeningen uitgevoerd met de hand, zoals met buigende momenten- en dwarskrachten. FEA software is gebaseerd op principes zoals traagheids- en weerstandsmomenten, elasticiteitsgrenzen, treksterkte, afschuifmodulus, hoofdspanningen en Von Mises spanningen. De komst van de computer heeft de schaal van de eindige elementenmethode enorm vergroot. De methode wordt al langer toegepast in geavanceerde sectoren, maar doordat de capaciteit van computers toeneemt en de eindige elementen softwareprogramma’s verbeteren en gebruiksvriendelijker worden, wordt deze techniek steeds toegankelijker voor analisten, ingenieurs én ontwerpers. De FEA software pakketten bestaan vaak uit een pre- en post processor en een aparte solver. Met een pre-processor maak je het model klaar voor de solver (de solver voert de analyses uit) en met de postprocessor kun je de analyseresultaten visualiseren en daarmee ook aan niet experts inzicht geven in het gedrag van de constructie. Bij Femto maken we o.a. gebruik van Femap, NX Nastran, Simcenter 3D en SDC Verifier, Abaqus en Optistruct voor het uitvoeren en visualiseren van onze analyses. Dit whitepaper geeft inzicht in de criteria voor een succesvolle FEA pre- en postprocessor selectie.

Toepassingen van FEA software

FEA software kan op meerdere manieren ingezet worden. Door de uiteindelijke gebruikssituatie van producten en constructies al vroeg in de ontwerpfase na te bootsen (simuleren), kunnen al vroeg ontwerpwijzigingen ten behoefte van sterkte aangebracht worden. Ook kunnen materiaalbesparingen worden gerealiseerd, bijvoorbeeld als er wanddikte teruggebracht kan worden. Bij productoptimalisaties is het de kunst om binnen een set van eisen (functionaliteit, esthetiek, etc.), met behulp van sterkteberekeningen naar de meest optimale vorm te zoeken.

FEA software wordt ook ingezet om constructies of producten te verifiëren volgens veiligheidsstandaarden. SDC Verifier is een voorbeeld van een FEA softwareprogramma dat hier speciaal voor ontwikkeld is. FEA wordt ook gebruikt om te onderzoeken waarom constructies falen. Tenslotte kunnen simulaties worden ingezet om de ontwerprichting te sturen. We noemen dit simulation driven design. Een goed voorbeeld hiervan is topologie optimalisatie. Door de toenemende eisen aan constructieve veiligheid, time-to-market en innovatie, zien we dat simulaties steeds meer worden toegepast. Een interessante ontwikkeling om in de gaten te houden is die van de digital twin.

»Terug naar legenda